Лабораторная работа.
Решение
задачи линейного программирования с помощью EXCEL
Задача
распределения ресурсов.
Тема:
использование возможностей табличного процессора Excel для решения задач
оптимизационного типа.
Цель: научиться решать задачи оптимизации средствами
табличного процессора Excel.
Варианты заданий
План:
1. Ознакомиться с общей постановкой задач оптимизационного типа.
2. Ознакомиться с особенностями работы с “Мастером функций”.
3. Научиться находить решение задач оптимизационного типа средствами Excel.
Теоретические сведения
Задача оптимизации формулируется как
нахождение оптимального (наибольшего, наименьшего, или такого, что равно
какому-то значению) значения определенной (целевой) функции (критерия) для определенной области изменения ее аргументов:
(область, как правило, определяется системой ограничений). Для решения задачи формируется ее математическая
модель, в электронную таблицу вносятся нужные данные, осуществляется поиск
оптимального решения.
Линейными
называются такие зависимости, в которые переменные входят в первой степени и с
ними выполняются только действия сложения или вычитания (имеются
ввиду действия между переменными, умножение, скажем, переменной на
константу не делает зависимость нелинейной).
Если же переменныe входят не в первой степени или с ними
выполняются другие действия, то зависимости являются нелинейными. При этом
следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то
и вся задача является нелинейной.
Задача
распределения ресурсов.
Если финансы, оборудование,сырье и даже людей
полагать ресурсами, то значительное число задач в экономике можно рассматривать
как задачи распределения ресурсов. Достаточно часто математической моделью
таких задач является задача линейного программирования (когда все зависимости модели являются линейными).
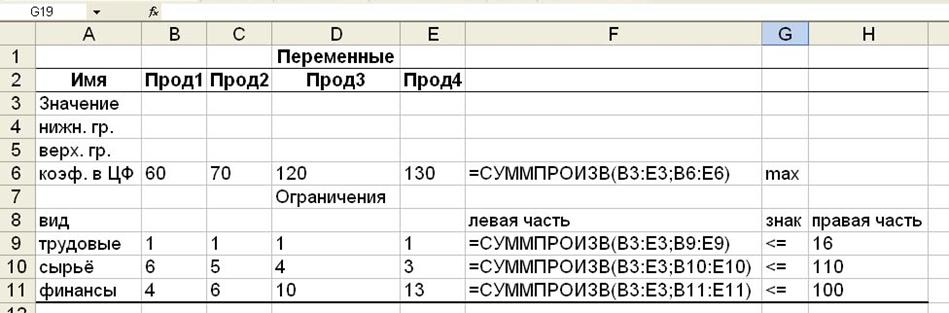
Рассмотрим следующий пример. Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведена на рис.1. Там же приведено наличие располагаемого ресурса.
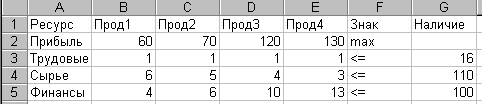
Рисунок 1.
Составим математическую модель, для чего
введем следущие обозначения:
xj - количество выпускаемой продукции j-го типа,
j=1,4;
bi - количество располагаемого ресурса i-го вида,
i=1,3;
aij - норма расхода i-го ресурса для выпуска
единицы продукции j-го типа;
cj - прибыль, получаемая от реализации единицы продукции
j-го типа.
Теперь приступим к составлению модели.
Как видно из рис.1, для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей
продукции Прод1 требуется 6 х1 единиц сырья, где х1
- количество выпускаемой продукции Прод1. С учетом того, что для других
видов продукции зависимости аналогичны, ограничение по сырью
будет иметь вид:
6х1+5х2+4х3<=110.
В этом ограничении левая часть равна величине
необходимого ресурса, а правая показывает количество
имеющегося ресурса. Аналогично можно составить ограничения для
остальных ресурсов и написать зависимость для целевой функции. Тогда математическая
модель задачи будет иметь вид:
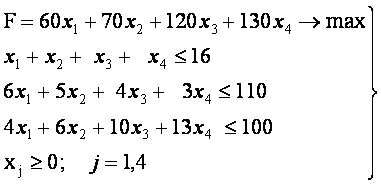
Создание формы и ввод исходных данных
представлены на рис.2.
Решение
задачи линейного программирования с помощью EXCEL
Работа с “Мастером
функций”
При введении функциональных
зависимостей можно использовать встроенные функции табличного процессора (таких
функций насчитывается около 400). (Можно также функциональные зависимости ввести и другими путями, например, – при
помощи клавиатуры). Вызов списка функций осуществляется активизацией команды : “Вставка/Функция…”. Можно также использовать соответствующую кнопку
панели инструментов – ![]() , которая носит
название "Мастер функций" и открывает окно диалога для выбора функции
и введения ее аргументов. Окно,
которое открывается, содержит: слева - список категорий, справа - список соответствующих функций.
Среди категорий отбирается тип функции – финансовая, математическая,
статистическая и тому подобное. Выбор типа функции сопровождается освещением в
правом окне списка функций, среди которого следует выбрать нужную.
После выбора функции освещается другое окно - “Мастер функции - шаг 2 из 2” с окнами
для введения списка аргументов. Активизацией кнопки "Ок" выбор функции и списка аргументов завершается.
, которая носит
название "Мастер функций" и открывает окно диалога для выбора функции
и введения ее аргументов. Окно,
которое открывается, содержит: слева - список категорий, справа - список соответствующих функций.
Среди категорий отбирается тип функции – финансовая, математическая,
статистическая и тому подобное. Выбор типа функции сопровождается освещением в
правом окне списка функций, среди которого следует выбрать нужную.
После выбора функции освещается другое окно - “Мастер функции - шаг 2 из 2” с окнами
для введения списка аргументов. Активизацией кнопки "Ок" выбор функции и списка аргументов завершается.
Примечание: если "щелкнуть" на поле
некоторого аргумента, в средней части окна появится информация
о его назначении.
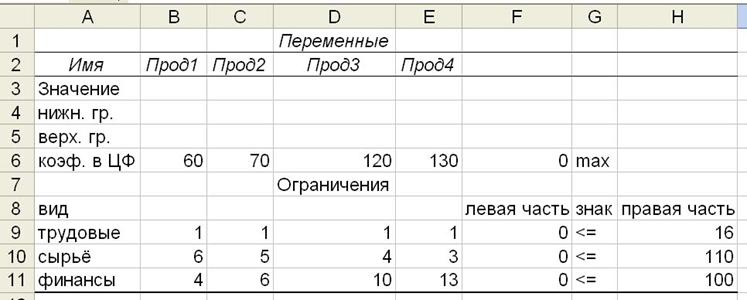
Рисунок
2.
Рассмотрим теперь
как ввести зависимость для целевой функции.
1. Сделать активной ячейку F6. (Клетку F6 назначим
базовой, в которую впоследствии будет заключено максимальное значение целевой
функции).
2. Щелкнем мышкой по мастеру функций.
Выберем категорию Математические.
Вызовем функцию СУММПРОИЗВ. Затем нажмите кнопку Далее. В окне диалога
(рис.3). В поле "Массив1" указываем блок ячеек
В3:Е3 (это ячейки, которые мы назначили
для дальнейшего вывода результатов – переменных х1
, х2 , х3 , х4), в поле "Массив2" – блок ячеек В6:Е6, в которых указаны коэффициенты целевой функции. Вместо функции СУММПРОИЗВ можно ввести саму сумму
произведений. Т.е. вместо формулы : =СУММПРОИЗВ(B3:E3; B6:E6) можно ввести : =B3*B6+C3*C6+D3*D6+E3*E6.
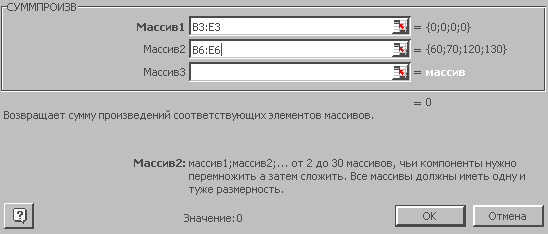
Рисунок
3.
3. Ввести зависимости для левых частей
ограничений.(рис.4).
Рисунок
4.
Замечание 1. Чтобы работать в режиме представления формул в
EXCEL необходимо выбрать СЕРВИС, ПАРАМЕТРЫ, на этой странице
в соответствующем поле выбрать отображать формулы.
Замечание 2. Т.к.
диапазаз ячеек B3:E3 в неизменном виде переходит из ячейки, скажем F9 ячейки F10 и F11, можно
скопировать
формулу из ячейки F9 в
ячейки F10
и F11 (перетаскивая содержимое ячейки F9 в ячейки F10 и F11 мышью). Но
для того, чтобы диапазаз ячеек B3:E3 не изменился, необходимо ввести знак $ в формуле – источнике (знак $ – признак
абсолютной ссылки). Т.е. в ячейке F9 вместо формулы =СУММПРОИЗВ(B3:E3; B6:E6 будет =СУММПРОИЗВ(B$3:E$3; B6:E6)
СОВЕТ. Во все диалоговые окна адреса ячеек удобно вводить не
с клавиатуры, а протаскивая мышь по ячейкам, чьи
адреса следует ввести.
Работа в диалоговом окне “Поиск решения”.
1. Установить целевую ячейку. Выбрать мышью ячейку F6.
2. Активизировать команду Сервис, Поиск
решения...
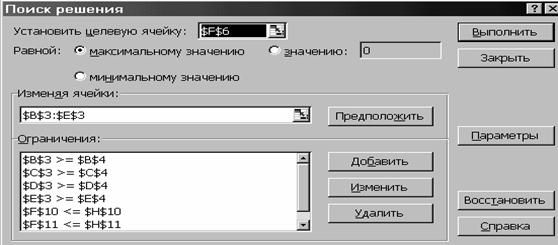
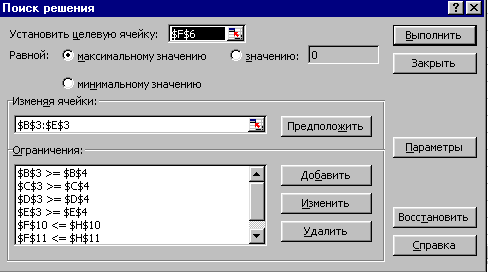 На рис.5 диалоговое окно поиск
решения.
На рис.5 диалоговое окно поиск
решения.
3. Убедиться, что в поле “Установить целевую ячейку”. Введён адрес F6.
4. Ввести направление целевой функции: Максимальному
значению.
5. Курсор в поле Изменяя ячейки. Ввести адреса B3:E3
(на рис.5 $B$3:$E$3).
Рисунок 5.
|
|
|
|
6.
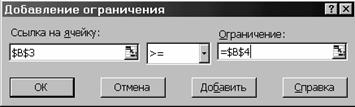
Добавить… (см. рис.5 и рис.6) После
нажатия кнопки “Добавить” открывается диалоговое окно "Добавление ограничения", в которое вносятся предельные условия
отдельно для каждой переменной F9<=H9, F10<=H10, F11<=H11 а также для B3>=B4, C3>=C4, D3>=D4, E3>=E4.
Т.к. в ячейках B4,C4, D4,
E4 ничего нет, то эти неравенства идентичны следующим :
B3>=0, C3>=0, D3>=0,
E3>=0. Их вообще можно указать в окне "Параметры поиска решения"
(см. п.7.), в установив
флажок “Неотрицательные значения”.
Рисунок 6 После
введения последнего ограничения выбрать кнопку “OK”. При этом окно "Поиск решения" с предельными условиями будет иметь следующий вид:
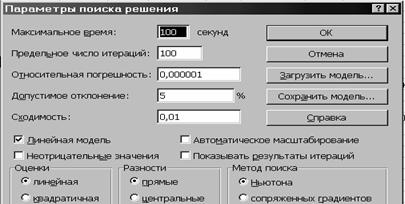
Рисунок 7 7. Удостоверившись в
правильности указанных ограничений, можно перейти к окну "Параметры поиска решения"
(выбрав кнопку “Параметры” см. рис.7.), в котором можно установить флажок
"Линейная модель", который обеспечит применения методу симплекса (быстрее поиск решения) и флажок “Неотрицательные
значения” ( вместо ограничений B3>=B4, C3>=C4, D3>=D4, E3>=E4 см. п. 6.).
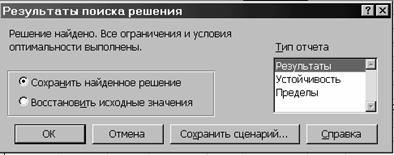
Рисунок 8 После нажатия кнопки OK, появится "Поиск решения", в котором нажатие кнопки "Выполнить" выводит на
экран окно "Результаты поиска решения" :
Рисунок 9 Оптимальное
решение для данной задачи найдено. Результаты решения вносятся в базу
данных после выбора параметра "Результаты". Конечным результатом работы
будет таблица : |
|
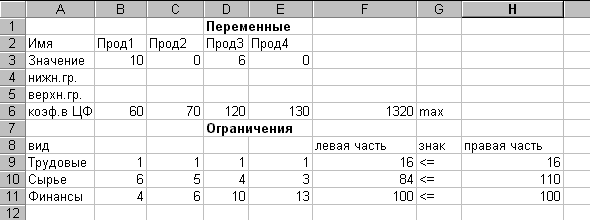
Рисунок 10
Анализ
полученного решения.
Из
рис.7 видно, что в оптимальном решении Прод1=В3=10,
Прод2=С3=0, Прод3=D3=6, Прод4=Е3=0.
При
этом максимальная прибыль будет составлять F6=1320 , количество использованных
ресурсов равно :
трудовых=F9=16,
сырья=F10=84, финансов=F11=100. Таково оптимальное решение
рассматриваемой задачи распределения ресурсов.
Ход работы
1. Ознакомиться с теоретической частью работы. Выяснить,
как формулируется задача оптимизационного типа, как формируется ее
математическая модель, как формируется таблица для развязывания задачи, в какой
последовательности и как вводятся данные, необходимые для развязывания задачи.
2. Выбрать вариант задания для выполнения, ознакомиться с
условием задачи. Определить, какие переменные и в каком количестве должны быть определенные, как они повязуються с другими данными задачи в форме критерія и в форме ограничений.
3. За условием задачи зформувати математическую модель.
Это должно быть система линейных неравенств и целевая функция.
4.
Загрузить
табличный процессор MicroSoft Excel.
5. Создать форму для введения условия задачи.
Предусмотреть введение имени переменных, их предельных значений (при
необходимости), коэффициентов целевой функции, системы ограничений – их левой и
правой части и соотношений между этими частями, самой целевой функции (см.
теоретическую часть, шаг первый).
6. Заполнить созданную форму данными – коэффициентами
целевой функции, коэффициентами системы линейных неравенств, свободными членами
системы линейных неравенств, соотношениями между левыми и правыми частями
неравенств (см. теоретическую часть, шаг второй).
7. Пользуясь "Мастером функций", ввести
зависимости в соответствия с
математической моделью, которые касаются целевой функции и левых частей системы
неравенств (см. теоретическую часть, шаг третий).
8. Вызывать диалоговое окно "Поиск решения", пользуясь соответствующей командой пункта
"Сервис". Установить: амбарчик с целевой функцией, направление
оптимизации, диапазон амбарчиков со значениями переменных, которые должны
определиться как решение задачи.
9. Вызывать диалоговое окно "Добавление ограничений", указать амбарчики, где находятся левые части
системы ограничений, условия их отношения к правым частям системы ограничений,
клетки, где находятся значения правых частей системы ограничений.
10. Убедиться, что в окне диалога с названием "Поиск решения" и "Параметры поиска решений" все
параметры выставлены правильно, перейти к решению задачи.
11. Прочитать и проанализировать результаты решения
задачи.
12. Оформить и сдать отчет по выполненной лабораторной
работе.
Контрольные
вопросы
1.
Какие типы данных
в задачах оптимизационного типа может содержать ячейка?
2.
Что являет собой
формула в задачах оптимизационного типа?
3.
В каких случаях и
как используются диапазоны в формулах?
4.
Как вставить
функцию в формулу?
5.
Назвать основные
категории "Мастера функций".
6.
Как вводятся
аргументы функций?
7.
Навести способы
ссылки на клетки. Привести пример относительных, абсолютных, смешанных ссылок.
8.
Что нужно указать
в окне "Поиск решения" меню
"Сервис"?
9.
Что нужно указать
в окне "Параметры поиска решения" ?
10. Как называется окно, где получены результаты решения?
Варианты заданий
Малое мебельне предприятие изготовляет стулья и кресла. Стоимость стула А гривен, стоимость кресла B гривен. Для их производства
используются материалы трех наименований : с1 кг.
– материала первого наименования, с2 кг. -
второго и с3 кг. – третьего наименования. Расходы этих материалов
составляют: на стул - а1 кг. материала первого наименования, а2 кг. – второго,
а3 кг. – третьего наименования; на кресло, соответственно, материала первого наименования - в1 кг., второго, - в2 кг., третьего, - в3 кг. Установить такой план
выпуска изделий, чтобы предприятие от их реализации получило максимальную
прибыль.
|
Вариант |
а1 |
а2 |
а3 |
в1 |
в2 |
в3 |
с1 |
с2 |
с3 |
А |
В |
|
1 |
20 |
15 |
14 |
28 |
9 |
1 |
758 |
526 |
541 |
10 |
12 |
|
2 |
19 |
3 |
9 |
13 |
25 |
3 |
571 |
577 |
445 |
5 |
10 |
|
3 |
11 |
13 |
13 |
21 |
5 |
4 |
741 |
710 |
822 |
5 |
3 |
|
4 |
14 |
12 |
8 |
18 |
14 |
22 |
624 |
541 |
375 |
7 |
16 |
|
5 |
19 |
16 |
19 |
26 |
17 |
8 |
850 |
638 |
853 |
5 |
21 |
|
6 |
14 |
15 |
20 |
40 |
27 |
4 |
740 |
742 |
822 |
6 |
9 |
|
7 |
9 |
11 |
15 |
27 |
15 |
3 |
606 |
802 |
840 |
11 |
16 |
|
8 |
13 |
13 |
11 |
23 |
25 |
4 |
608 |
672 |
575 |
7 |
5 |
|
9 |
8 |
19 |
14 |
7 |
8 |
1 |
417 |
580 |
591 |
9 |
12 |
|
10 |
19 |
16 |
21 |
32 |
18 |
16 |
760 |
524 |
540 |
10 |
12 |
|
11 |
12 |
14 |
23 |
22 |
6 |
5 |
751 |
456 |
841 |
8 |
17 |
|
12 |
15 |
21 |
27 |
10 |
8 |
9 |
909 |
932 |
880 |
7 |
8 |
|
13 |
17 |
16 |
11 |
13 |
19 |
23 |
967 |
685 |
755 |
21 |
29 |
|
14 |
23 |
26 |
31 |
7 |
9 |
11 |
267 |
309 |
385 |
8 |
7 |
|
15 |
25 |
32 |
38 |
11 |
15 |
18 |
298 |
318 |
374 |
20 |
26 |
Разработка-дизайн
(публикации в web) :
Федунець А.Д., Оришака О.В.